Moving the mirror a distance of
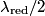 causes the fringe pattern to shift by a distance equal to the distance between two fringes. Therefore, if the fringe pattern shifts so that causes the fringe pattern to shift by a distance equal to the distance between two fringes. Therefore, if the fringe pattern shifts so that 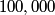 fringes pass across the detector for green light, the mirror must have moved a distance fringes pass across the detector for green light, the mirror must have moved a distance 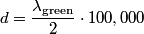 The same argument can be applied to the red laser, therefore 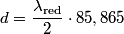 We can combine the two equations above to give: 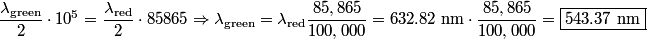 Therefore, answer (B) is correct. |